선형계획법 - 최대화문제

선형계획법 - 최대화문제

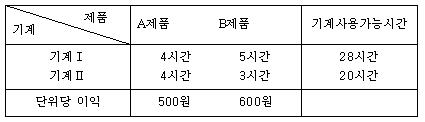
이 기업의 이익최대화를 위한 A,B제품의 생산수량결정

① 선형계획을 구성하고

② 도식해법으로 풀어라

(도표 8) 제조에 관한 자료

(풀이)

① 모형의 구성 ; A제품 생산량 X, B제품 생산량을 Y라 할 때

최대화 Z = 500X + 600Y

제약조건 4X + 5Y ≤28……………………………………①

4X + 3Y ≤20……………………………………②

X,Y ≥0

② 도식해법 ; 제약식 ①, ②를 직선식으로 변형하면

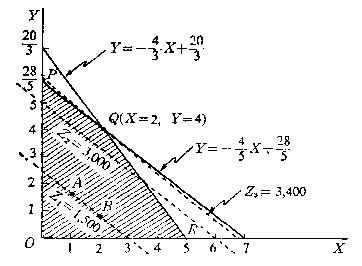
이들 ③, ④식을 그래프화하면 (도표 4)이고, 식 ①, ②에서 부등호가 “≤”이므로 빗금부분이 가해영역임.

(도표 4) 최대화 문제의 도식해법

그리고 목함수를 Y에 관해 표시함으로써 등이익선을 구한다.

식 ⑤에서 등이익선의 기운기는 -5/6이고 Y축에 대한 절편은 Z/600이다.

* 등이익신이란 X, Y의 값이 어떻게 결합되든 간에 동일 이익을 나타내는 점들로 이루어진 선임.

예를 들어

* 등이익선은 (X=3, Y=0)일 때의 이익이 1500원이고, (X=0, Y=2.5)일 때의 이익이 1,500원이므로 그 두 점을 연결하는상의 점은 X와 Y의 값이 어떻게 결합되어도 (예컨데 A, B) 모두 1,500원이 이익을 발생시킴.

* 최적해는 총이익이 최대가 되는 점에서 실현됨.

* 총이익은 -5/6의 기울기를 가지는 등이익선이 원점에서 멀어질수록 커지게 됨.

* 제약조건을 고려한 최적해는 가해영역중의 원점에서 가장 먼 꼭지점과 등이익선이 접하는 점(X=2, Y=4)에서 실현됨

* 식 ③, ④를 연립시켜 풀면 X=2, Y=4이므로 최적해는 X=2단위, Y=4단위임.

* 이 때의 순이익 Z=500(2)+600(4)=3,400원

출처 : 최신공장관리기술사(하권) OR 출판사 : (주)ATPM컨설팅

저자 : 공학박사/기술사/지도사 권오운 지음

공장혁신/공장기술사 자료실 메인 페이지로 홈페이지 메인으로