게임이론 - 혼합전략

게임이론 - 혼합전략

다음 (도표 78)은 어느 기업의 사장과 종업원대표간의 임금인 상형상을 보여준다. 이익행렬은 종업원대표(A)에게 이익을, 사장(B)에게 손실을 나타낸다.

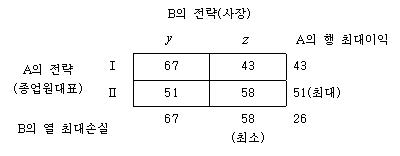
종업원 대표는 종업원의 이익을 최대화하고, 사장은 이러한 값(즉, 기업에 대한 손실)을 최소화하기를 원한다.

(도표 79) 종업원 대표와 사장의 이익행렬

(1) 본문은 순수전략의 경우인가, 혼합전략의 경우인가, 그 이유는?

(2) 수식에 의하여 최적해를 구하라.

(풀이)

(1) 전략의 종류 및 이유

본문은 게임을 위한 공통값, 즉 안점이 존재 안하므로 혼밥전략 선택함

맥시민원리에 의하면, A는 최소액을 최대화하기 위하여 전략 Ⅱ를 선택하고, B는 최대손실을 최소화하기 위해 전략을 z를 선택할 것이다.그러나 B는 즉각 불만할 것이다.

이는 A가 Ⅱ를 선택시 B가 z에서 y로 이동함 에 따라 그의 손실을 51로 감소할 수 있기 때문이다. 따라서 B는 y를 선택한다. B의 y에 대해 A는 Ⅰ을 선택하여 67의 이익을 얻으려 할 것이다. A의 Ⅰ에 대해 B는 z를 선택하여 손실을 43으로 감소시키려 할 것이다. 그러면 다시 A는 원래의 Ⅱ로 되돌아가 순환을 계속하게 된다.

이와 같이 맥시민(미니맥스)원리에 의하면 두사람은 언제나 불만에 차 있다. 이러한 경우에는 균형이 나타나지 않으므로 A와 B가 게임의 값을 가지기 위해서는 혼합전략을 택해야 한다. 최적해는 수식이나 도표에 의해 구할 수 있다.

(2) 수식에 의한 해법(대수해법)

① A의 경우A는 B가 y를 선택함으로써 발생하게 될 기대이익과 z를 선택함으로서 나타나게 될 기대이익을 동일하게 하는 방향에서 자기의 전략 Ⅰ과 Ⅱ를 사용하는 확률을 결정할 것이다.

만일 A가 확률로서 전략 Ⅰ을, (1-)의 확률로서 전략 Ⅱ를 선택시B가 y를 선택한다고 하면 A의 기대이익은 이 됨.