|
1. 모집단과 표본
통계학에서의 모집단(population)이란 용어는 매우 특별한 의미를 갖는다. 이는 연구대상이 되는 물체나
사람들의 총제를 의미하며, 여기서 표본이 택해진다. 예를 들어 대통령 선거결과를 예측하기 위하여 여론조사를 하는 경우 대상 모집단은 한국인
유권자 전체가 된다. 모집단의 크기는 문제에 따라 달라진다. 어떤 대학의 특수한 학과를 대상으로 학생의 평균적인 몸무게를 알고자 한다면 그
학과의 학생수(예를들어 100명)가 모집단의 크기가 될 것이다.
표본에 속한 각 관측값이 무작위로 택해졌을 때 이 표본을 무작위 표본(또는 확률 표본, 랜덤표본, random
sample) 이라고 한다. 만약 표본이 무작위로 뽑혔다면 여기에 속한 임의의 한 관측값은 모집단의 성격을 그대로 갖게 된다. 즉 다음이
성립한다.
무작위 표본에 속한 각 관측값의 확률분포 p(x)는 모집단의 확률분포와 동일하다.
통계학을 이해하는데 가장 중요한 기본용어는 母集團(population)과 標本(sample)이다.
통계학에서
말하는 모집단은 관심의 대상이 되는 모든 개체의 관측값이나 측정값의 집합을 의미한다. 따라서 모집단에 대한 어떤 성질을 언급하고자 할 때는, 그
모집단을 구성하는 각 개체의 성질을 뜻하는 것이 아니고 모집단이라고 하는 하나의 전체에 대한 전반적인 특성을 뜻한다. 또한 통계적 처리를 위하여
모집단에서 실제로 추출된 관측값이나 측정값의 집합을 표본이라고 한다. 즉 표본은 모집단의 특성을 잘 나타낼 수 있는 모집단의 부분집합니다.
여러분은 全數調査라는 단어를 흔히 접하게 되는데 이는 모집단 전체를 조사하는 것이다.
모집단은 그것을 구성하는 크기에 따라서 유한모집과 무한모집단으로 나눌 수 있다. 즉 모집단이 유한개의 관측값이나
측정값의 집합이면 有限母集團(finite pop-ulation)이라 하고, 무한개의 집합이면 無限母集團(infinite
population)이라고 한다.. 그러나 유한개의 관측값의 집합이라 할지라도 상당히 큰 모집단이면 대체로 무한모집단의 성격을 갖는 것으로
간주하게 된다. 2. 기술통계량(Descriptive Statistics)
통계학의 주요 목적은 표본자료를 이용하여 모집단의 특성을 추론하는데 연구자의 관심에 따라 실험 또는 관찰을 통해
얻어지는 실현값을 자료(data)라 한다. 따라서 자료는 연구자의 연구 목적 및 특성에 따라서 다음과 같이 분류할수 있다.
- 수량자료(numerical data) - 숫자로 표시될수 있는 자료
[예]
연속형자료(continuous data) : 키, 몸무게, 시간 등
이산형자료(discrete data) : 인구수,
불량품 수 등
- 범주형자료(categorical data) - 설문을 통해 얻어지는 자료
[예] 성별, 주거형태,
찬반여부 등
- 시계열자료(time series data) - 시간의 흐름에 영향을 받는 자료
[예] 물가, 물가지수
등
- 횡단자료(cross sectional data) - 특정 시점에서 여러 가지 특성을 조사한 자료
만약 자료의 값이 GNP, 매출액, 경제성장률, 수출입현황, 임금, 키, 몸무게, 제품의 수명, 교통사고 건수 등과
같이 수치로 나타내어질 때는 양적자료라 하고, 산업분류, 채권분류, 성별, 생활수준, 지역분류, 종교성향, 교육수준 등과 같이 자료 그 자체가
수치로 표시할 수 없는 자료를 질적 자료 혹은 범주형 자료라고 한다.
통계적 분석은 관심의 대상이 되는 표본자료가 수집되면 그 특성을 알아보는 것으로부터 시작된다.
표본의 특성은 도수분포표(frequency table)나 여러 가지 그림표에 의하여 나타낼 수도 있으며,
표본통계량(sample statistic)에 의하여 표현 할 수 있게 된다.
양적 자료의 정보를 수치적으로 나타내는 방법은 여러가지가 있지만 가장 많이 이용하는 방법으로 중심위치의 측도,
비대칭 측도 등을 생각할 수 있다. 중심위치의 측도는 주어진 자료가 어떤 값을 중심으로 분포되어 있는가를 나타내는 것이며, 산포의 측도는
자료들이 중심위치에서 얼마만큼 퍼져있는가를 알려준다. 비대칭 측도는 자료의 분포가 대칭에서 벗어나서 어느 방향으로 얼마나 치우쳐 있는가를 알 수
있게 한다. 3. 중심위치 측도
자료의 중심위치를 나타내는 대표값을 측정하는 방법에는 평균, 중앙값, 최비값 등이 가장 널리 사용되고 있다.
그리고 이 세 가지 대표값 중에서 어떤 것을 자료의 대표값으로 선택할 것인가는 그 자료의 성격과 연구목적에 따라
달라질 수 있다.
평 균
여기서 다루는 평균(mean)이란 산술평균을 의미하며 자료의 중심위치를 나타내는 대표값으로 가장 널리 사용되고
있다.
산술평균은 기술통계뿐만 아니라 추측통계에서도 매우 중요한 역할을 한다. 산술평균이란 모든 자료의 값을 더하여 자료의
개수로 나눈 값을 의미한다.
우리가 표본으로 취한 n개의 자료값을 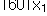 , , 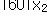 , …, , …, 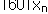 으로 표시하면, 평균은 다음과 같이 정의된다. 으로 표시하면, 평균은 다음과 같이 정의된다.
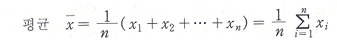
흔히 통계학에서 다루는 평균계산은 주어진 자료가 모집단일 때의 평균과 표본일때의 평균으로 구분하여 생각하여야 한다.
모집단과 표본을 구별하기 위하여 모집단의 자료 수를 N, 모집단의 평균을 모평균(population mean)
μ(Greek 문자로서 '뮤'라고 읽는다), 표본의 자료 수를 n, 표본의 평균을 표본평균(sample mean)  ('엑스바아')라고 한다. ('엑스바아')라고 한다.
모평균과 포본평균의 계산방식은 다음과 같다.
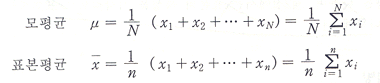
중앙값
관찰된 자료의 중심위치 측도에서 산술평균 다음으로 중요한 용어가 중앙값(median)이다.
중앙값은 숫자로 표시된 양적 자료에만 사용되는 것으로서 그 의미는 다음과 같다.
중앙값은 자료를 크기순으로 나열할 때 가운데 위치하는 자료값을 말한다.
자료의 수를 n이라 할 때 크기 순서대로 나열된 자료값을 순서통계량(order statistics)이라 하며
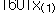 , , 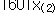 , …, , …, 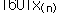 로 표시한다. 여기서 로 표시한다. 여기서 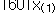 은 자료의 최소값이고 은 자료의 최소값이고 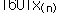 은 자료의 최대값이다. 은 자료의 최대값이다.
자료의 중앙값을 결정하기 위하여는 다음과 같은 과정을 거치게 된다.
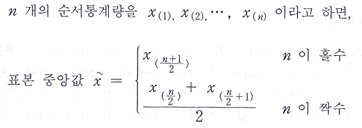
최빈값
최빈값(mode)은 질적 자료나 양적 자료 모두에 사용되며 자료의 분포에서 빈도수가 어느 곳에 가장 많이 밀집되어
있는가를 측정하는 것이다.
최빈값은 자료에 따라 존재하지 않을 수도 있으며, 또한 존재하더라도 유일하지 않을 수도 있다.
또한 최빈값은 앞에서 다룬 대표값과는 달리 양적인 자료보다는 질적 자료의 분석에 더 효과적으로 이용될 수 있다.
예를 들면, 소비자의 상품 구매 충동이 어떤 광고 매체를 통하여 이루어졌는가를 조사하여 최빈값을 구하여 가장
효율적인 광고매체를 결정할 수 있을 것이다.
세 통계량의 특징
평
균
- 자료 관측값의 산술평균이다.
- 각 자료에 있어서 유일하게 구하여진다.
- 소수의 매우 크거나 작은 값에 의하여 영향을 받는다.
- 자료를 몇 개의 작은 집단으로 나누었을 때 각 집단의 평균의 평균은 전체자료를 이용하여 구한 평균과 같다.
중위수
- 중앙위치의 값으로 관측값의 50%가 왼쪽에 그리고 나머지 50%가 오른쪽에 존재한다.
- 각 자료에 있어서 유일하게 구하여진다.
- 소수의 매우 크거나 작은 값에 의하여 영향을 받지 않는다.
- 자료를 몇 개의 작은 집단으로 나누었을 때 각 집단의 중위수의 중위수는 전체자료를 이용하여 구한 중위수와 항상
일치하지는 않는다.
- 수량으로 관측된 자료에만 이용가능하다.
최빈값
- 자료에서 관측빈도의 수가 가장 많은 값이다.
- 각 자료에서 하나 이상의 최빈값이 있을 수 있다.
- 소수의 극한값에 영향을 받지 않는다.
- 자료를 몇 개의 작은 집단으로 나누었을 때 각 집단의 최빈값에 의하여 전체의 최빈값을 유도할 수
없다.
- 양적으로 측정된 자료와 질적으로 측정된 자료 모두에 이용 가능하다.
4. 산포도 측도
지금까지 자료의 대표값에 대하여 비교·검토하였다.
그러나 자료의 대표값으로 자료의 중심위치는 측정할 수 있으나, 자료들이 어떠한 형태로 분포되어 있는지를 알 수가
없다.
예를 들어 두 자료의 분포에 대한 평균이 같다고 하더라도 분포의 형태는 다를 수 있는 경우가 있다.
따라서 자료이 분포에 대한 특성을 알아보기 위하여는 중심위치와 더불어 각 자료값들이 평균과 같이 대표값 주위에
흩어져 있는 정도를 측정하는 산포도(measure of dispersion)에 관한 추가적인 정보기 필요하다.
산포도를 측정하는 방법은 범위(range), 분산(variance), 표준편차(standard deviation),
사분위간 범위(inter-quartile range), 변동계수(coefficient of variation) 등이 있으나 여기서는 산포도로서
널리 사용되는 분산과 표준편차 그리고 변동계수에 대하여 설명하고자 한다.
분산과 표준편차
자료가 모집단일 때의 분산을 모분산(population variance)이라 하며 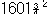 (시그마 제곱)이라 표기하고 이때의 표준편차를 모표준편차(population standard deviation)라 하고 σ(시그마)라
표기한다. (시그마 제곱)이라 표기하고 이때의 표준편차를 모표준편차(population standard deviation)라 하고 σ(시그마)라
표기한다.
한편, 자료가 표본일 때의 분산을 표본분산(sample variance)이라 하고 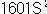 으로 표기하고, 이때의 표준편차를 표본표준편차(sample standard deviation)라 하고 S로
표기한다. 으로 표기하고, 이때의 표준편차를 표본표준편차(sample standard deviation)라 하고 S로
표기한다.
이들이 계산공식은 다음과 같이 정의된다.
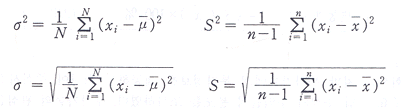
변동계수
변동계수(coefficient of variation)는 여러 종류의 자료의 산포도를 비교하는데 사용되어진다.
만약 두 자료의 평균이 같다면 각 자료의 표준편차를 비교함으로써 어느 자료의 분포가 상대적으로 넓게 퍼져있는지를
판단할 수 있을 것이다.
그러나 두 자료의 평균이 서로 다를 때에는 표준편차만을 비교함으로써 두 자료의 상대적인 산포의 정도를 측정할 수는
없다.
따라서 서로 다른 평균과 표준편차를 갖는 여러 자료의 상대적인 변동 혹은 산포를 측정하기 위해서는 각 자료의 평균과
표준편차를 동시에 고려한 변동계수가 유용하게 사용되어지며, 다음과 같이 정의된다.
변동계수 : υ = (S / 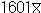 ) × 100% ) × 100%
왜 도
지금까지는 주어진 자료의 대표값과 산포도가 측정되면 이러한 특성치를 통하여 자료의 중심위치 및 퍼져있는 정도를
파악할 수 있었으나, 분포의 특성을 좀더 적절하게 설명하기 위해서는 자료가 좌우 대칭분포인가, 혹은 한 쪽으로 얼마나 치우친 분포인가를 측정하는
것이 필요하다.
자료의 분포가 기울어진 방향과 정도를 나타내는 척도를 왜도(skewness)라고 하며, 피어슨의 왜도
계수(pearsonian coefficient of skewness)는 다음과 같이 정의된다.

이 값이 양(음)의 값을 가지고 있을 때는 오른쪽(왼쪽)으로 기울어져 있다고 할 수 있으며 그림으로 나타내면 다음과
같다.
피어슨의 왜도계수에 의하여 산출된 왜도값에 따라 분포모양의 특징을 다음과 같이 해석할 수 있다.
만약
왜도가 0이면 (a)의 경우와 같이 좌우 대칭인 분포를 이룬다. 왜도가 양수이면 (b)의 경우와 같이 오른쪽에 긴 꼬리가 있고, 왼쪽에는 짧은
꼬리를 갖는 비대칭 분포를 나타낸다. 반대로 왜도가 음수이면 (c)의 경우와 같이 왼쪽에 긴 꼬리가 있고, 오른쪽에는 짧은 꼬리를 갖는 비대칭
분포를 나타낸다.
또한 분포의 형태에 따라서 중심위치를 측정하는 대표값들의 위치가 달라지기 때문에 분포의 형태와 대표값들의 위치를
비교하여 보기로 하자. (a)와 같이 분포가 대칭일 경우에는 평균, 중앙값, 최빈값은 일치하지만, (b)와 같이 양의 왜도분포는 오른쪽 꼬리에
다른 대부분의 자료값보다 매우 큰 값이 존재 하기 때문에 왜도분포는 오른쪽 꼬리에 다른 대부분의 자료값보다 매우 큰 값이 존재하기 때문에 평균은
중앙값에 비하여 커지게 되어 최빈값 < 중앙값 < 평균 의 관계가 성립된다.
그리고 (c)와 같이 음의 왜도분포는 왼쪽
꼬리에 다른 대부분의 자료값보다 매우 작은 값이 존재하기 때문에 평균은 중앙값에 비하여 작아지게 되어 평균 < 중앙값 < 최빈값 의
관계가 성립하게 된다.
|
